Gravity with torsion as deformed BF theory

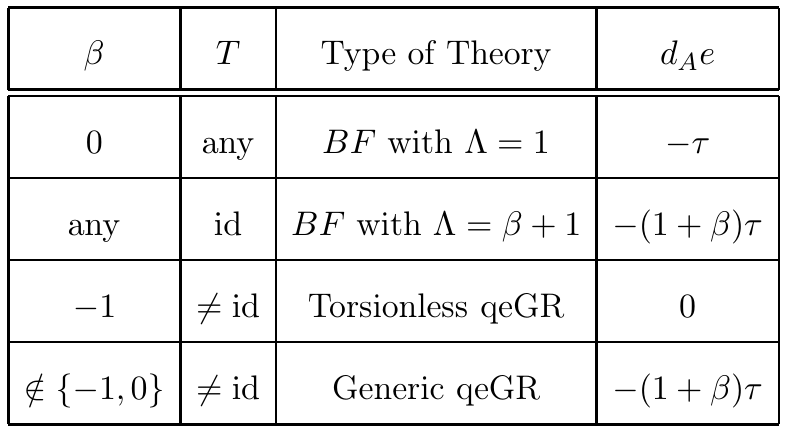
This paper contains the results of my master thesis under supervision of Alberto Cattaneo and Michele Schiavina. In it we study a family of – possibly non topological –deformations of $BF$ theory for the Lie algebra obtained by quadratic extension (following [1,2]) of $\mathfrak{so}(3,1)$ by an orthogonal module.

The resulting theory – which we called quadratically extended General Relativity (qeGR) – is shown to be classically equivalent to certain models of gravity with dynamical torsion. The classical equivalence is shown to promote to a stronger notion of equivalence within the Batalin–Vilkovisky formalism.

In particular, both Palatini–Cartan gravity and a deformation thereof by a dynamical torsion term, called $(\textit{quadratic})$ generalised Holst theory, are recovered from the standard Batalin–Vilkovisky formulation of qeGR by elimination of generalised auxiliary fields.

The paper is available to read on the arxiv.
The manuscript has since been published in Classical and Quantum Gravity with open access.

qeGR_action
qeGR_table
Prev
Neutron Stars in Einstein–Cartan Theory
Next
2D Topological Quantum Field Theory

Selected Works

Homotopy Transfer and Graph TheoryArticle

Neutron Stars in Einstein–Cartan TheoryArticle

Quadratically Extended GRArticle

2D Topological Quantum Field TheoryArticle

Mathematical Aspects of Classical and Quantum Field TheoryLecture Notes

AKSZ TheoriesProject

AKSZ BF TheoryProject

Contact

Email: info[]leonmenger[]de
Github: /Leon-Menger
LinkedIn: /leonmenger
ORCID: 0000000306214977

© Leon Menger 2023

Website built with OCD