Homotopy Transfer and Graph Theory
Last semester I had the pleasure of writing a small exposé for a course on discrete mathematics. The idea was to provide a brief but hopefully comprehensive introduction to the application of graph theory in the homotopy transfer of algebraic structures.
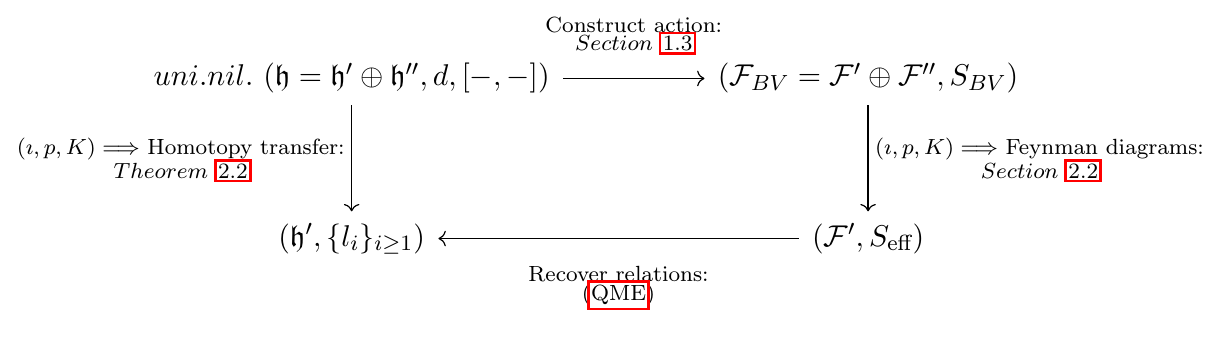
Making this more niche for mathematicians but possibly much more interesting for physicists, the whole text uses BF theory – a field theory – to illustrate the constructions. In particular it shows how BF theory can and should be seen as a generating function for an algebraic structure.
Using a splitting of fields into "slow" and "fast" field components, one then obtains Feynman rules. These are building blocks for graphs that constitute an effective BF action, where only "slow" field components remain and the "fast" ones are integrated out. To translate these graphs and the whole effective action back to a generating function for some algebraic structure is the main and most interesting point of the text.
The exposé provides ample references for much deeper introductions to its constituent topics and none of its parts are in any way new work. I hope however that it can serve as a recounting of a familiar story or even a link between known topics for some. The file can be downloaded here.
Selected Works
Contact
Email: info[]leonmenger[]de
Github: /Leon-Menger
LinkedIn: /leonmenger
ORCID: 0000000306214977
© Leon Menger 2023
Website built with OCD